Cono: EL CONO

CLASIFICACIÓN:

Se denominan:

Cono recto, si el vértice equidista de la base circular
Cono oblicuo, si el vértice no equidista de su base
Cono elíptico, si la base es una elipse. Pueden ser rectos u oblicuos.

La generatriz de un cono es cada uno de los segmentos cuyos extremos son el vértice y un punto de la circunferencia de la base.
La altura de un cono es la distancia del vértice al plano de la base. En los conos rectos será la distancia del vértice al centro de la circunferencia de la base.

PROPIEDADES:

Área de la superficie cónica

El área $A\,$ de la superficie del cono recto es:

$A=A_{Base}+ A_{Lateral}=\pi r^2 + \pi rg\,\!$

donde r es el radio de la base y g la longitud de la generatriz del cono recto.

La generatriz de un cono recto equivale a la hipotenusa del triángulo rectángulo que conforma con la altura del cono y el radio de la base;
su longitud es: $g=\sqrt{h^2+r^2}\,$ .

Desarrollo plano de un cono recto

Desarrollo plano del cono.

El desarrollo plano de un cono recto es un sector circular y un círculo.
El sector circular está delimitado por dos generatrices, siendo la medida del lado curvo igual a la longitud de la circunferencia de la base.
La forma de calcular la distancia a en el desarrollo es con la ecuación de $a=\sqrt{h^2+r^2}\,$
donde r es el radio de la base y h es la altura del cono.
El ángulo que está sombreado en la figura se calcula con la siguiente fórmula:

$\mathrm{\acute{a}ngulo} = 360(r/a) \,$ .

Volumen de un cono

El volumen $V\,$ de un cono de radio $r \,$ y altura $h \,$ es 1/3 del volumen del cilindro que posee las mismas dimensiones:

$V = \frac{\pi \cdot r^2 \cdot h}{3}\,\!$

La ecuación se obtiene mediante $\int^{h}_{0}A(x)dx\,\!$ ,
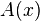donde $A(x)\,$ es el área de la sección perpendicular a la altura, con relación a la altura $h$ , en este caso $A(x)=\pi\left(\frac{rx}{h}\right)^2$ .

CONO OBLICUO:

Secciones de un cono recto y un cono oblicuo de base circular.

Un cono oblicuo es aquel cono cuyo eje de revolución no es perpendicular a su base.
Pueden ser de dos tipos: de base circular o de base elíptica. El de base elíptica es el cuerpo geométrico resultante de cortar un cono recto mediante un plano oblicuo a su eje de revolución.
La base es un círculo o una elipse, y la altura es el segmento que contiene al vértice, siendo perpendicular al plano de la base; pero no es coincidente con el eje del cono.

Superficie y desarrollo

La superficie lateral de un cono oblicuo es un triángulo curvilíneo, con dos generatrices por lados y base semi-elíptica.
La superficie de la base de un cono oblicuo es un círculo o una elipse.

Volumen

La ecuación empleada para hallar el volumen de un cono oblicuo de base circular es similar a la del cono recto:

$V = \frac{\pi r^2 h} {3}$

donde $\scriptstyle r$ es el radio de la base y $\scriptstyle h$ la altura del cono oblicuo. La ecuación del volumen de un cono oblicuo de base elíptica es:

$V = \frac{\pi a b h}{3}$

Cono

martes, 15 de abril de 2014

EL CONO