CONO:
martes, 15 de abril de 2014
TEMA 13 (APARTADO 3)
Un cuerpo redondo es la figura que se obtiene al girar una forma plana una vuelta completa alrededor de un eje situado en el mismo plano.
CONO:

CONO:
EL CONO
CLASIFICACIÓN:
Se denominan:
La altura de un cono es la distancia del vértice al plano de la base. En los conos rectos será la distancia del vértice al centro de la circunferencia de la base.

 de la superficie del cono recto es:
de la superficie del cono recto es:
La generatriz de un cono recto equivale a la hipotenusa del triángulo rectángulo que conforma con la altura del cono y el radio de la base;
su longitud es: .
.
El desarrollo plano de un cono recto es un sector circular y un círculo.
El sector circular está delimitado por dos generatrices, siendo la medida del lado curvo igual a la longitud de la circunferencia de la base.
La forma de calcular la distancia a en el desarrollo es con la ecuación de
donde r es el radio de la base y h es la altura del cono.
El ángulo que está sombreado en la figura se calcula con la siguiente fórmula:

 de un cono de radio
de un cono de radio  y altura
y altura  es 1/3 del volumen del cilindro que posee las mismas dimensiones:
es 1/3 del volumen del cilindro que posee las mismas dimensiones:
 ,
,
donde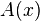 es el área de la sección perpendicular a la altura, con relación a la altura
es el área de la sección perpendicular a la altura, con relación a la altura  , en este caso
, en este caso  .
.
Un cono oblicuo es aquel cono cuyo eje de revolución no es perpendicular a su base.
Pueden ser de dos tipos: de base circular o de base elíptica. El de base elíptica es el cuerpo geométrico resultante de cortar un cono recto mediante un plano oblicuo a su eje de revolución.
La base es un círculo o una elipse, y la altura es el segmento que contiene al vértice, siendo perpendicular al plano de la base; pero no es coincidente con el eje del cono.
La superficie de la base de un cono oblicuo es un círculo o una elipse.
 es el radio de la base y
es el radio de la base y  la altura del cono oblicuo. La ecuación del volumen de un cono oblicuo de base elíptica es:
la altura del cono oblicuo. La ecuación del volumen de un cono oblicuo de base elíptica es:
Se denominan:
- Cono recto, si el vértice equidista de la base circular
- Cono oblicuo, si el vértice no equidista de su base
- Cono elíptico, si la base es una elipse. Pueden ser rectos u oblicuos.
La altura de un cono es la distancia del vértice al plano de la base. En los conos rectos será la distancia del vértice al centro de la circunferencia de la base.

PROPIEDADES:
Área de la superficie cónica
El área de la superficie del cono recto es:
de la superficie del cono recto es:La generatriz de un cono recto equivale a la hipotenusa del triángulo rectángulo que conforma con la altura del cono y el radio de la base;
su longitud es:
 .
.Desarrollo plano de un cono recto
Desarrollo plano del cono.
El sector circular está delimitado por dos generatrices, siendo la medida del lado curvo igual a la longitud de la circunferencia de la base.
La forma de calcular la distancia a en el desarrollo es con la ecuación de

donde r es el radio de la base y h es la altura del cono.
El ángulo que está sombreado en la figura se calcula con la siguiente fórmula:
.

Volumen de un cono
El volumen de un cono de radio
de un cono de radio  y altura
y altura  es 1/3 del volumen del cilindro que posee las mismas dimensiones:
es 1/3 del volumen del cilindro que posee las mismas dimensiones: ,
,donde
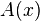 es el área de la sección perpendicular a la altura, con relación a la altura
es el área de la sección perpendicular a la altura, con relación a la altura  , en este caso
, en este caso  .
.CONO OBLICUO:
Un cono oblicuo es aquel cono cuyo eje de revolución no es perpendicular a su base.
Pueden ser de dos tipos: de base circular o de base elíptica. El de base elíptica es el cuerpo geométrico resultante de cortar un cono recto mediante un plano oblicuo a su eje de revolución.
La base es un círculo o una elipse, y la altura es el segmento que contiene al vértice, siendo perpendicular al plano de la base; pero no es coincidente con el eje del cono.
Superficie y desarrollo
La superficie lateral de un cono oblicuo es un triángulo curvilíneo, con dos generatrices por lados y base semi-elíptica.La superficie de la base de un cono oblicuo es un círculo o una elipse.
Volumen
La ecuación empleada para hallar el volumen de un cono oblicuo de base circular es similar a la del cono recto:donde
 es el radio de la base y
es el radio de la base y  la altura del cono oblicuo. La ecuación del volumen de un cono oblicuo de base elíptica es:
la altura del cono oblicuo. La ecuación del volumen de un cono oblicuo de base elíptica es:lunes, 14 de abril de 2014
RESUMEN DEL TEMA 11
1-ÁNGULOS DE UN POLÍGONO
- La suma de los ángulos interiores de un triángulo es 180º.
- La suma de los ángulos interiores de un polígono de x lados es 180º · (x-2)
- Si el polígono de x lados es regular, todos suas ángulos interiores son iguales y su medida es 180º · (x-2) / x
2-FIGURAS SEMEJANTES
- Dos triángulos son semejantes si sus ángulos son iguales y sus lados son proporcionales.
- Dos polígonos son semejantes si sus ángulos son iguales y sus lados son proporcionales.
6-TRIÁNGULOS: RECTAS Y PUNTOS NOTABLES
- Mediatrices y circuncentro: las mediatrices de un triángulo son las mediatrices de cada uno de sus lados. Se cortan en un punto, el circuncentro, que está situado a igual distancia de los tres vértices y es el centro de la circunferencia circunscrita.
- Bisectrices e incentro: las bisectrices de un triángulo son las bisectrices de cada uno de sus ángulos. Se cortan en un punto, el incentro, que está situado a igual distancia de los tres lados y es el centro de la circunferencia inscrita.
- Medianas y baricentro: las medianas de un triángulo son las rectas que pasan por cada vértice y por el punto medio del lado opuesto. Se cortan en un punto, el baricentro, cuya distancia al vértice es doble que su distancia al punto medio del lado opuesto.
- Alturas y ortocentro: las alturas de un triángulo son las rectas perpendiculares trazadas desde cada vértice al lado opuesto a su prolongación. Las alturas se cortan en un punto llamado ortocentro.
- Alturas y ortocentro: las alturas de un triángulo son las rectas perpendiculares trazadas desde cada vértice al lado opuesto a su prolongación. Las alturas se cortan en un punto llamado ortocentro.
7-LONGITUDES Y ÁREAS DE FIGURAS POLIGONALES
Rectángulo: A= a · b
Paralelogramo: A= b · h
Rombo: A= D · d / 2
Triángulo: A= b · h / 2
Trapecio: A= (B+b) · h / 2
Polígono regular: A= P · a / 2
8-LONGITUDES Y ÁREAS DE FIGURAS CIRCULARES
Longitud: arco circunferencia: L= 2π · r · nº / 360º
Área: sector circular: A= π · r² · nº / 360º
corona circular: A= π · (R² - r²)
trapecio circular: A= π · nº · (R² - r²) / 360º
Suscribirse a:
Entradas (Atom)




